알고리즘의 시간 복잡도와 Big-O 쉽게 이해하기
삼성역에서 택시를 타고 강남역으로 향했는데 30분 걸렸다. 구글에서 알려주는 최단경로로 갔더라면 15분내에 도착할 것이다. 레스토랑을 예약해서 가는 경우라던지 친구와 약속시간을 잡은경우 우리에게는 시간은 항상 소중하다. 그래서 우리는 시간을 효율적으로 사용하기위한 노력을 의식적으로 하고 있다.
컴퓨터 프로그래밍에서도 시간복잡도가 가장 낮은 알고리즘을 채택해 이러한 상황을 개선하고 있다. 택시를 타고 삼성역까지 가는 절차를 알고리즘이라고 하는데 이때 수행하는 연산의 수를 시간복잡도로 나타낸다. 택시를 타고 강남역까지 가는 과정을 알고리즘으로 표현하면 아래와 같다.
function TakeTaxy(from, to) {
/*
1. 차량에 탑승한다.
2. from에서 to까지 최단거리 루트를 선택한다.
3. 목적지까지 가는 루트을 설명한다.
4. 출퇴근 시간의 경우 차가 막히는 루트는 피한다.
5. 출발하는동안
6. 만약 적색 신호등이면 정지한다.
7. 만약 녹색 신호등이면 출발한다.
8. 도착하면
9. 요금을 정산한다.
10. 차량에서 내린다.
*/
}
따라서 알고리즘이란
- 어떤 목적을 달성하거나 결과물을 만들어내기 위해 거쳐야 하는 일련의 과정들을 의미한다.
- 가는 루트는 다양하며 여러가지 상황에 따른 알고리즘은 모두 다르다. 따라서 시간복잡도가 가장 낮은 알고리즘을 선택하여 사용한다.
여기서 알고리즘의 실행시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존한다.
이 속도는 컴퓨터의 처리속도, 사용된 언어종류, 컴파일러의 속도에 달려있다.
알고리즘의 실행시간을 두 부분으로 나누면
- 입력값의 크기에 따라 알고리즘의 실행시간을 검증해볼 수 있다.
- 입력값의 크기에 따른 함수의 증가량, 우리는 이것을 성장률이라고 부른다.
이때 중요하지 않는 상수와 계수들을 제거하면 알고리즘의 실행시간에서 중요한
성장률에 집중할 수있는데 이것을 점금적 표기법(Asymptotic notation)이라 부른다.
여기서, 점근적이라는 의미는 가장 큰 영향을 주는 항만 계산한다는 의미다.
점근적 표기법은 다음 세가지가 있는데 시간복잡도를 나타내는데 사용된다.
- 최상의 경우 : 오메가 표기법 (Big-Ω Notation)
- 평균의 경우 : 세타 표기법 (Big-θ Notation)
- 최악의 경우 : 빅오 표기법 (Big-O Notation)
평균인 세타 표기를 하면 가장 정확하고 좋겠지만 평가하기가 까다롭다.
그래서 최악의 경우인 빅오를 사용하는데 알고리즘이 최악일때의 경우를 판단하면 평균과 가까운 성능으로 예측하기 쉽기때문이다.
빅오 표기법(Big-O)
빅오 표기법은 불필요한 연산을 제거하여 알고리즘분석을 쉽게 할 목적으로 사용된다.
Big-O로 측정되는 복잡성에는 시간과 공간복잡도가 있는데
- 시간복잡도는 입력된 N의 크기에 따라 실행되는 조작의 수를 나타낸다.
- 공간복잡도는 알고리즘이 실행될때 사용하는 메모리의 양을 나타낸다.
요즘에는 데이터를 저장할 수 있는 메모리의 발전으로 중요도가 낮아졌다. - 아래는 대표적인 Big-O의 복잡도를 나타내는 표이다.
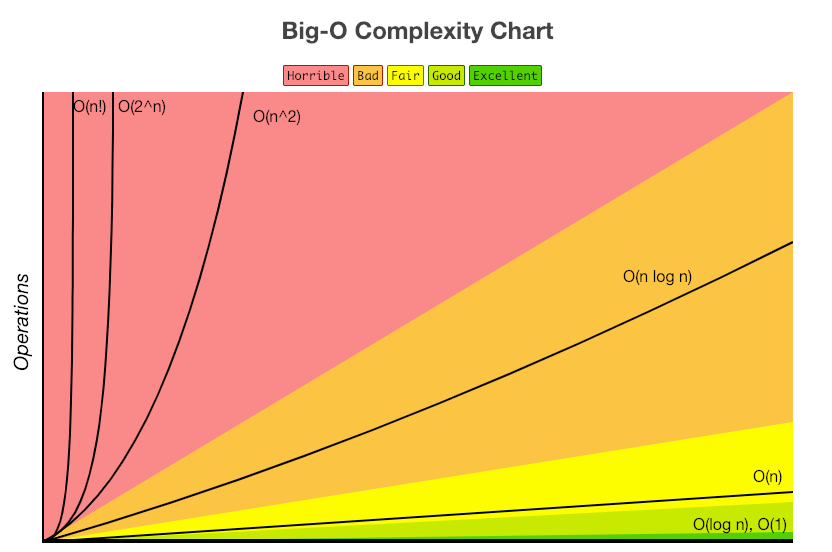
시간복잡도
시간복잡도의 가장 간단한 정의는 알고리즘의 성능을 설명하는 것이다.
다른의미로는 알고리즘을 수행하기 위해 프로세스가 수행해야하는 연산을 수치화 한것이다.
왜 실행시간이 아닌 연산수치로 판별할까? 위에도 설명했지만 명령어의 실행시간은 컴퓨터의 하드웨어 또는 프로그래밍 언어에 따라 편차가 크게 달라지기 때문에 명령어의 실행 횟수만을 고려하는 것이다.
시간복잡도에서 중요하게 보는것은 가장큰 영향을 미치는 n의 단위이다.
1 O(1) --> 상수
2n + 20 O(n) --> n이 가장 큰영향을 미친다.
3n^2 O(n^2) --> n^2이 가장 큰영향을 미친다.
시간복잡도의 문제해결 단계를 나열 하면 아래와같다.
O(1) – 상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
O(log n) – 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
O(n) – 직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
O(n log n) : 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼의 수행시간을 가진다. (선형로그형)
O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
O(C^n) – 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱.
아래표는 실행시간이 빠른순으로 입력 N값에 따른 서로 다른 알고리즘의 시간복잡도이다.
| Complexity | 1 | 10 | 100 |
|---|---|---|---|
| O(1) | 1 | 1 | 1 |
| O(log N) | 0 | 2 | 5 |
| O(N) | 1 | 10 | 100 |
| O(N log N) | 0 | 20 | 461 |
| O(N^2) | 1 | 100 | 10000 |
| O(2^N) | 1 | 1024 | 1267650600228229401496703205376 |
| O(N!) | 1 | 3628800 | 화면에 표현할 수 없음! |
O(1) : 상수
아래 예제 처럼 입력에 관계없이 복잡도는 동일하게 유지된다.
def hello_world():
print("hello, world!")
O(N) : 선형
입력이 증가하면 처리 시간또는 메모리 사용이 선형적으로 증가한다.
def print_each(li):
for item in li:
print(item)
O(N^2) : Square
반복문이 두번 있는 케이스
def print_each_n_times(li):
for n in li:
for m in li:
print(n,m)
O(log n) O(n log n)
주로 입력 크기에 따라 처리 시간이 증가하는 정렬알고리즘에서 많이 사용된다.
다음은 이진검색의 예이다.
def binary_search(li, item, first=0, last=None):
if not last:
last = len(li)
midpoint = (last - first) / 2 + first
if li[midpoint] == item:
return midpoint
elif li[midpoint] > item:
return binary_search(li, item, first, midpoint)
else:
return binary_search(li, item, midpoint, last)
시간복잡도를 구하는 요령
각 문제의 시간복잡도 유형을 빨리 파악할 수 있도록 아래 예를 통해 빠르게 알아 볼수 있다.
- 하나의 루프를 사용하여 단일 요소 집합을 반복 하는 경우 : O (n)
- 컬렉션의 절반 이상 을 반복 하는 경우 : O (n / 2) -> O (n)
- 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복 할 경우 : O (n + m) -> O (n)
- 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O (n²)
- 두 개의 중첩 루프를 사용하여 두 개의 다른 콜렉션을 반복 할 경우 : O (n * m) -> O (n²)
- 컬렉션 정렬을 사용하는 경우 : O(n*log(n))
정렬 알고리즘 비교
Sorting Algorithms |
공간 복잡도 | 시간 복잡도 |
||
|---|---|---|---|---|
최악 |
최선 |
평균 |
최악 |
|
| Bubble Sort | O(1) | O(n) | O(n2) | O(n2) |
| Heapsort | O(1) | O(n log n) | O(n log n) | O(n log n) |
| Insertion Sort | O(1) | O(n) | O(n2) | O(n2) |
| Mergesort | O(n) | O(n log n) | O(n log n) | O(n log n) |
| Quicksort | O(log n) | O(n log n) | O(n log n) | O(n2) |
| Selection Sort | O(1) | O(n2) | O(n2) | O(n2) |
| Shell Sort | O(1) | O(n) | O(n log n2) | O(n log n2) |
| Smooth Sort | O(1) | O(n) | O(n log n) | O(n log n) |
자료구조 비교
Data Structures |
Average Case |
Worst Case | ||||
|---|---|---|---|---|---|---|
| Search | Insert | Delete | Search | Insert | Delete | |
| Array | O(n) | N/A | N/A | O(n) | N/A | N/A |
| Sorted Array | O(log n) | O(n) | O(n) | O(log n) | O(n) | O(n) |
| Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Doubly Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Stack | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Hash table | O(1) | O(1) | O(1) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log n) | O(log n) | O(log n) | O(n) | O(n) | O(n) |
| B-Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| Red-Black tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| AVL Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
